On a vacation to Iceland, you happened upon a small museum dedicated to Bobby Fischer. You got interested in Chess and Chess Sets, and you happened to learn that New Chess Sets often come with extra queens in case a pawn is promoted to a second queen. Bobby Fischer even played a famous game where the players had two queens each!
Anyway, this got you thinking … what could you do with all of those extra Queens? Maybe try to place them on the board at the same time, in a way that no Queen could attack any other? Since Queens move horizontally, vertically, and diagonally in both directions, this is not as easy as it sounds.
Even on a smaller 4×4 chessboard it’s not obvious. At first glance, it’s easy to see that one will have at most 4 queens on a 4×4 chessboard, since there can be a single queen per row or column.
![Rendered by QuickLaTeX.com \chessboard[ printarea=a1-d4, setwhite={Qc4,Qa3,Qd2,Qb1}, showmover=false ]](https://www.patternsandlies.com/wp-content/ql-cache/quicklatex.com-e1d08ccc63ea70a3fb8b7d5e3ed81777_l3.png)
In fact, each Queen is on a different row, a different column, different lower left to upper right diagonal (ascending), and upper left to lower right diagonal (descending).
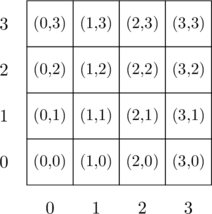
We can use this to form equations that form constraints for Queen placement Each equation represents a line with exactly one Queen.
(1) 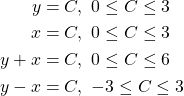
We then just walk through the possibilities, placing one Queen at a time. If we get stuck, we backtrack out.
func solveNQueens(n int) [][]string {
var result [][]string
columns := make([]int, n)
positive := make([]int, 2*n-1)
negative := make([]int, 2*n-1)
board := make([][]rune, n)
for r := 0; r < n; r++ {
board[r] = make([]rune, n)
for c := 0; c < n; c++ {
board[r][c] = '.'
}
}
var solver func(r int)
solver = func( row int) {
for col := 0; col < n; col++ {
if columns[col] != 0 || positive[row+col] != 0 || negative[n-1+row-col] != 0 {
continue
}
board[row][col]='Q'
if row + 1 >= n {
var answer []string
for _, row := range board {
answer = append(answer, string(row))
}
result = append(result, answer)
} else {
columns[col]++
positive[row+col]++
negative[n-1+row-col]++
solver(row+1)
columns[col]--
positive[row+col]--
negative[n-1+row-col]--
}
board[row][col]='.'
}
}
solver(0)
return result
}